Als je de kranten mag geloven kun je artificiële intelligentie werkelijk overal toepassen. Van tekst herkennen, tot de diagnose van borstkankergezwellen. Hoe komt het dat deze technologie zo breed inzetbaar is? In zijn "eerste iBestuur-college":https://ibestuur.nl/magazine/onbekendheid-met-ai-vertroebelt-debat benadrukte professor Chris Verhoef dat AI een vorm van statistiek is, en dat een prozaïsche naam als zelflerend niets anders betekent dan het vinden van de beste coëfficiënten, zodat de fout van de antwoorden zo klein mogelijk is.
Beeld: Colin Behrens / Pixabay
Bij statistiek werk je over het algemeen met voorgebakken aannames. Zo van: tussen deze twee variabelen kan weleens een kwadratisch verband zitten. Vervolgens gebruik je iets als Excel om de beste parabool te vinden. Als het verband ingewikkelder wordt, moet je eerst een idee hebben van hoe dat verband eruit kan zien, en dan kun je met een iets ingewikkeldere methode hetzelfde procedé uitvoeren.
In het eerste college is uitgelegd dat een onderliggend algoritme – de statistische hint over wat het verband kan zijn – niet bij elk probleem te bedenken valt: niet vooraf en ook vaak niet achteraf. Bij klassieke statistiek zijn het juist die vragen waarop je toch een soort antwoord moet hebben, om daarna het beste voorgebakken model te kunnen selecteren. AI is juist van toegevoegde waarde als het soort model zich niet laat raden.
1. De universele benaderingsstelling
Dat onbekende verband om bijvoorbeeld letters te kunnen herkennen, hangt af van zo’n 15 variabelen. Het onbekende verband is dus één of andere continue functie in de 15-dimensionale ruimte. Maar we weten totaal niet welke. Je gooit er plaatjes in, die zet je om naar 15 getallen, en die bepalen dan welke letters het betreft. En met diezelfde methode kun je ook kwaadaardig celweefsel detecteren.
Er is een belangrijk resultaat uit de wiskunde dat ten grondslag ligt aan de universele toepasbaarheid van AI. Dit resultaat zegt ruwweg dat elke n-dimensionale continue functie te benaderen is met een eindig aantal eenvoudige zenuwcellen. Hoe dit precies zit voert te ver, maar het is mogelijk om het aan de hand van eenvoudige voorbeelden te illustreren. Zodra de methode erachter duidelijker is, zal ook duidelijk worden dat je moet oppassen met het toepassen van gevonden algoritmes in andere contexten. Dit is iets waar de discussie over AI ook over gaat, en soms is dat terecht, soms ook niet. Meer begrip van de onderliggende theorie, geeft handvatten om de discussie beter te voeren.
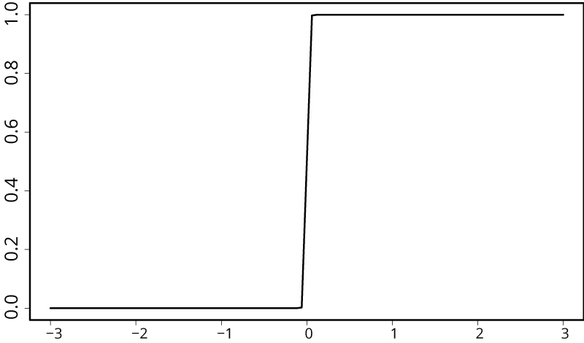
Figuur 1: Van 0 naar 1
Je kunt je voorstellen dat een zenuwcel als een schakelaartje werkt; hij kan van uit naar aan als de cel getriggerd wordt. Zie figuur 1. Daar is een eenvoudige zogeheten logistische functie getekend: door een gebeurtenis gaat de trigger af en gaat hij van 0 naar 1. Zo’n trigger kan ook ongedaan gemaakt worden en dan ga je van aan naar uit, of van het getal 1 naar 0: figuur 2.
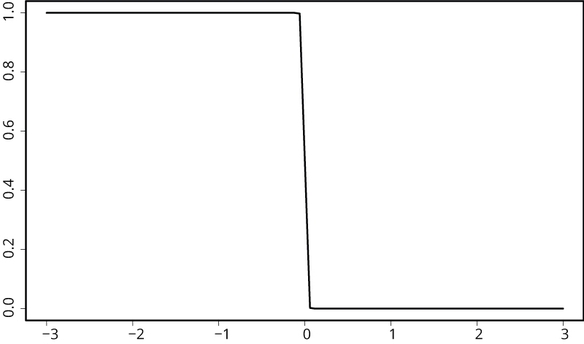
Figuur 2: Van 1 naar 0
Als we deze twee figuren combineren door ze van elkaar af te trekken, maken we daarmee een hele korte spijkerfunctie: die is de hele tijd 0 maar heel even is de functie gelijk aan 1. Dat is in figuur 3 weergegeven.
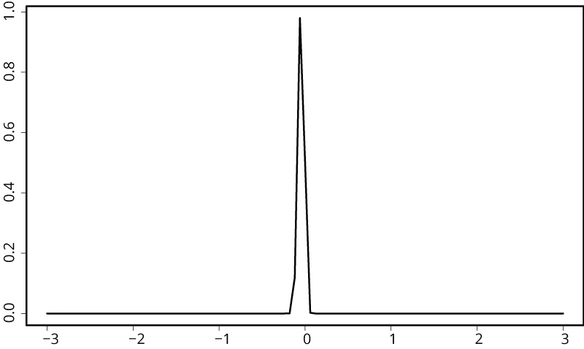
Figuur 3: Van nul naar een en weer terug
Door de functie met 3 te vermenigvuldigen krijg je een spijker die tot 3 oploopt, en door hem door -2 te delen krijg je juist een spijker die even op een half onder 0 zit. Met een eindig aantal van deze spijkerfuncties kun je dan elk verband altijd benaderen. In figuur 4 is daar een voorbeeld van gegeven. Daar is een onbekend soort verband weergegeven dat zo complex is dat je niet kunt weten wat het precies is. Maar door geduldig overal spijkers langs te leggen kun je het complexe verhaal terugbrengen tot een honderdtal spijkers, die elk op zich te begrijpen zijn.
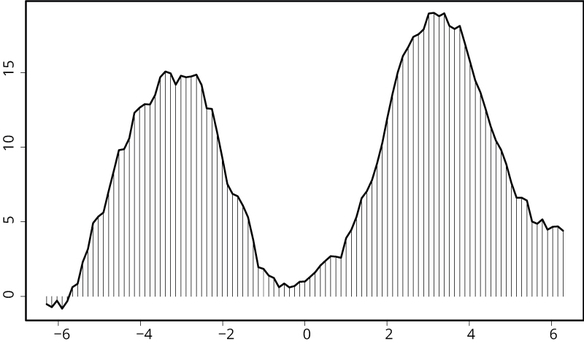
Figuur 4: Onbekend verband benaderd met spijkerfuncties
De crux van de universele approximatiestelling is dat een neuraal netwerk, dus een samenstel van eenvoudige lineaire vergelijkingen met een triggerfunctie eromheen, in staat is om elke continue functie in de n-dimensionale ruimte heel goed te benaderen met een eindig aantal zenuwcellen. Vandaar ook de term universeel. En het bijzondere is dat je het verband van te voren niet hoeft te raden zoals in klassieke statistiek. Dat is een extreem krachtig wiskundig resultaat. En juist dat resultaat zorgt ervoor dat je AI te pas en te onpas kunt toepassen.
2. Leren kwadrateren
Stel er is een verband tussen twee variabelen: input en output. In tabel 1 staat het verband genoemd voor 13 waarden. We hebben voor de input -3 tot en met 3 het kwadraat genomen en dat is onze output. In de klassieke statistiek vermoed je een soort kwadratisch verband en op basis van die voorkennis probeer je de beste parabool te vinden.
| input | output | |
| -3 | 9 | |
| -2.5 | 6.25 | |
| -2 | 4 | |
| -1.5 | 2.25 | |
| -1 | 1 | |
| -0.5 | 0.25 | |
| 0 | 0 | |
| 0.5 | 0.25 | |
| 1 | 1 | |
| 1.5 | 2.25 | |
| 2 | 4 | |
| 2.5 | 6.25 | |
| 3 | 9 |
Tabel 1: Het geobserveerde verband tussen input en output
In de AI sla je die eerste stap over. Zonder je af te vragen om welk verband tussen input en output het zou kunnen gaan, zoek je gelijk het beste verband vanuit de data. In dit geval is er 1 input en 1 output, dus dat is een simpel model, en voor het gemak nemen we er eentje met 3 zenuwcellen en 1 tussenlaag (dus weinig diepgang).
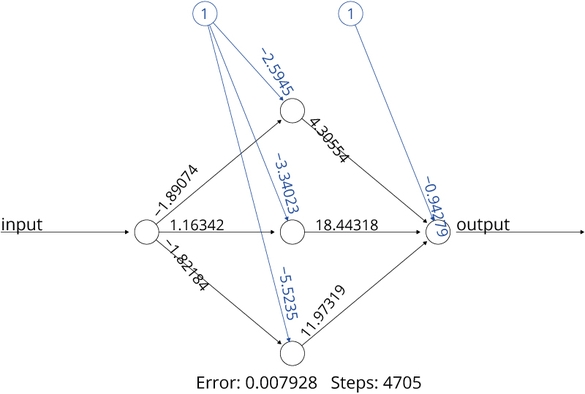
Figuur 5: Datagedreven model voor kwadrateren
Met behulp van de gegevens uit de tabel leren we van de paar zenuwcellen hoe de vork in de steel zit. En daaruit wordt een netwerk gevonden met de structuur zoals in figuur 5. De coëfficiënten zijn in de eerste stap random gekozen en door herberekenen en het minimaliseren van de fout tussen input en output zijn ze na 4705 stapjes geconvergeerd naar een model dat op de 13 waarden een hele kleine foutmarge heeft van nog geen achtduizendste (zie ook het eerste college).
In figuur 6 tekenen we de data, het gevonden model en de parabool waaruit we de data hebben ‘opgekweekt’. De gegevens uit de tabel zijn in de figuur met groen aangegeven. Een echte parabool is in rood getekend, en het neurale netwerk is gevoed met 600 waarden tussen -3 en +3 en het blijkt dat het de parabool nagenoeg feilloos weet te imiteren.
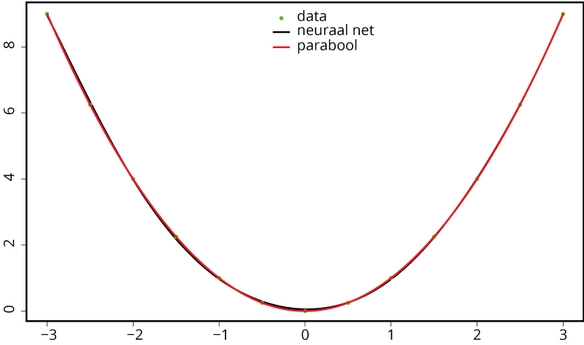
Figuur 6: Neuraal net leert parabolen tekenen
3. Begrijpbaarheid versus analyseerbaarheid
Als het verband tussen input en output niet begrijpbaar is door als mens naar de data te kijken, dan heb je met deze statistische methode toch een alternatief om het verband op basis van de input te vinden, en er ook voorspellingen mee te doen. Maar het gevonden verband moet je wel degelijk eerst analyseren voordat je het gaat toepassen.
Hoe realistisch is het model in verschillende contexten? Want er zit een addertje onder het gras. De zesde figuur is in feite een analyse van het gevonden algoritme: we tekenen het en vergelijken het met de parabool en zo zien we dat het gevonden model de kwadratische functie heel aardig weet te imiteren. Realiseer je echter wel dat het model niet echt weet wat kwadrateren is. Daarom moet je zulke modellen met beleid toepassen, want voor je het weet gebruiken mensen het waar het niet voor bedoeld is.
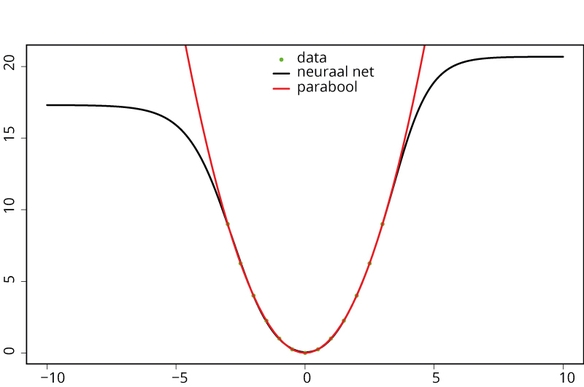
Figuur 7: Neuraal net weet niet wat een parabool is
In figuur 7 is te zien hoe het dan mis kan gaan. In deze figuur is het model toegepast op data buiten het bereik van de trainingsset. Het gevonden algoritme vertelt in de figuur wat het denkt dat de waardes tussen de -10 en +10 zijn. Zodra je buiten de -3 of +3 komt gaat het steeds erger mis: links en rechts buigt het af naar een horizontale eindstand. Die delen van de zesde figuur lijken erg op de eerste twee figuren: de aan/uit functies. Dit is niet zo gek want het idee van de universele benaderingstelling is dat je met dat soort functies het verband probeert te benaderen, en deze twee horizontale uiteinden zijn daar de uitvloeisels van.
De kunst bij het gebruik van deze technieken is om te zorgen dat nieuwe gevallen dicht genoeg bij de inleergevallen zitten zodat de voorspellingen realistisch zijn. Een recent voorbeeld waarin dit niet werkte is het Chinese algoritme dat besluit of een coronapatiënt naar de ic moet of niet. Dat bleek in Nederland niet te werken omdat het ingeleerd was met scanners met een hogere stralingsdosis dan in Nederland. Het zag in Nederland het verschil niet tussen een longontsteking door corona of anderszins. Voordat het in gebruik werd genomen is het eerst geanalyseerd, en net als de parabool: als je het buiten het inleerbereik toepast krijg je de verkeerde resultaten.
Dit artikel staat ook in iBestuur magazine 36



Ha Chris,
Als hiermee iets duidelijk wordt is het wel dat KI, m.i.v. een al dan niet ruimere bruikbaarheid van algoritmen, tenminste door een modale lezer als deze eenvoudig nauwelijks nog te begrijpen valt. Daarmee is (onbedoeld) de belangrijkste boodschap van je artikel misschien wel dat we dat ook maar niet meer moeten proberen. En dat is nu precies het grote maatschappelijke probleem van KI waarvoor ik bijzondere aandacht vraag in mijn weblog “De Nationale AI-Cursus: grote stappen, snel thuis….”)
Slechts weinigen, en dan voornamelijk ook nog eens beta’s, begrijpen hoe KI werkt. Een overgrote meerderheid doet dat niet en heeft er ook nog eens geen enkel zicht op waarvoor KI inmiddels allemaal al wordt en nog zal worden ingezet. Dat laatste klemt temeer aangezien de ontwikkeling van KI grotendeels binnen de hoge muren van de grote Techbedrijven plaatsvindt, politiek en overheid die ontwikkelingen niet (kunnen) controleren terwijl het wel om zeer ingrijpende toepassingen (met tamelijk curieuze onderliggende filosofieën) kan gaan. Wat rest is blind vertrouwen in degenen die het nog begrijpen en dat is dan ook precies waar de EC, die het ongetwijfeld zelf al veel langer niet meer begrijpt, om vraagt (ik citeer: “Trust is a prerequisite to ensure a human-centric approach to Artficial Intelligence.”). Fraaie retoriek zij het in de verkeerde volgorde van een instituut waarvan menigeen zich terecht zal afvragen of dat nu de eerst aangewezene is om ons om vertrouwen te vragen.
Lees daarom s.v.p. ook mijn blog en laat mij nog eens weten of je iets voelt voor zo’n brede maatschappelijke discussie die ook over risico’s en maatschappelijke consequenties van de ontwikkeling en inzet van KI zou moeten gaan. Velen mogen dan niet meer kunnen begrijpen hoe KI werkt, voor veel potentiele toepassingen geldt dat voorlopig nog even niet. En gelukkig maar…
Beste groet,
Ruud